logo
Typescript

Canvas 공 충돌 시뮬레이션 프로젝트 정리글

문성석2022년 8월 1일

결과물

preview



프로젝트 설명

이 프로젝트는 Canvas 내에서 여러 개의 공들이 움직이고 서로 충돌하는 시뮬레이션을 구현한 것이다. 각 공은 최초 랜덤한 속도와 방향으로 움직이며, 화면 경계와 다른 공에 부딪힐 때 반사되도록 구현하였다. 프로젝트 소스 코드는 여기 Github 저장소에 정리해놨다.



사용한 기술

HTML Canvas와 Typescript를 사용하였다. Canvas를 이용해 그래픽 요소를 동적으로 구현하였고, Typescript로 각 공의 움직임 및 충돌 감지 기능들을 구현하였다.



프로젝트에서 배운 것들

1) 공 생성에 필요한 랜덤 숫자 구한 방법

프로젝트에서는 초기에 공들의 크기와 위치를 랜덤으로 설정하여 다양한 시작 상태를 만들어내고자 했다. 이를 위해 최소 숫자와 최대 숫자를 인자로 받아 그 사이의 랜덤한 숫자를 반환하는 getRandomNumber 함수를 구현했다. 이 함수는 프로젝트 전체에서 사용될 가능성이 높아 Utils 클래스에 모듈화하여 활용하였다.

// utils.ts
 
export default class Utils {
  /**
   * 주어진 최소값(min)과 최대값(max) 사이의 랜덤 정수를 반환합니다.
   * @param min - 반환할 랜덤 숫자의 최소값
   * @param max - 반환할 랜덤 숫자의 최대값
   * @returns min과 max 사이의 랜덤 정수
   */
  static getRandomNumber(min: number, max: number): number {
    // Math.random()은 0 이상 1 미만의 난수를 생성합니다.
    // 이를 활용하여 (max - min + 1) 범위의 난수를 얻고, 이를 min에 더하여 최종적으로 min과 max 사이의 정수를 반환합니다.
    return Math.floor(Math.random() * (max - min + 1)) + min;
  }
}

이후 공들을 생성하는 makeBalls 함수에서 필요한 랜덤한 숫자들을 얻을 수 있었다.

private makeBalls(): void {
  let balls = [];
 
  // 랜덤으로 공 10 ~ 20개 생성
  for (let i = 0; i < Utils.getRandomNumber(10, 20); i++) {
    // 랜덤 반지름, 좌표 생성
    const radius = Utils.getRandomNumber(10, 20);
    const x = Utils.getRandomNumber(radius * 2, this.canvas.width - radius * 2);
    const y = Utils.getRandomNumber(radius * 2, this.canvas.height - radius * 2);
 
    ...
  }
 
  this.balls = balls;
}

2) 랜덤한 방향으로 공을 보내는 방법

공 생성까지는 모두 완료했는데, 이제는 랜덤한 방향으로 공을 보내는 작업을 구현해야 했다. 이 작업을 구현하기 위해서는 크기 1을 가지고 랜덤한 방향을 가진 단위 벡터가 필요했다.

이 랜덤한 방향을 가진 단위 벡터는 랜덤 Radian 값을 활용하여 다음과 같이 구현하였다.

const radian = Math.random() * Math.PI * 2
const unitVector = new Vector(Math.cos(radian), Math.sin(radian))
 
* Radian이란?
- 각도 측정 단위 중 하나로, 원주 위의 호의 길이에 따라 각을 측정하는 방법.
- 일반적으로 1 라디안은 약 57.2958도에 해당하지만, 이 프로젝트에서 약 60도로 생각하고 계산
 
* 랜덤 Radian 값 구한 방법
- Math.random 메소드를 사용하여 0과 1 사이의 난수를 생성하고,
  랜덤 Radian 값으로 변환하기 위해 원주율에 2를 곱한 값을 다시 곱함
 
* Vector 클래스는 x와 y 값으로 구성된 2차원 벡터 클래스
- 프로젝트 작업을 위해 따로 추상화 진행

여기서 구한 단위 벡터를 방향으로 하여 랜덤한 방향으로 공을 보낼 수 있었다.



3) 공 충돌 기능 구현 방법


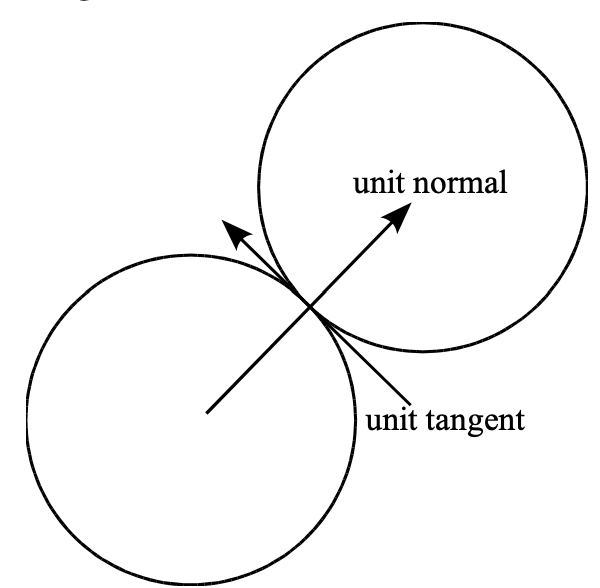
collision formula
  1. 두 공의 벡터를 이용하여 un(unit normal)과 ut(unit tangent)를 구한다.
  2. 만약 unit normal의 길이가 두 공의 반지름을 더한 값과 작거나 같아진다면, 충돌로 인식
  3. un, ut와 두 공이 충돌하기 전의 속도를 이용하여 반사되는 스칼라 값을 구한다.
  4. 아래 공식을 이용하여 충돌 이후, 반사되는 속도를 구한다. (여기서 m은 mass인데 질량 관련된 속성은 없으니 반지름으로 대체)
  5. 3번과 4번에서 계산한 충돌 이후 반사되는 스칼라, 속도를 결합하여 벡터 생성
  6. 각각의 공에 새롭게 생성된 벡터를 할당하여 다시 반사된 방향으로 이동


참고

2-Dimensional Elastic Collisions Without Trigonometry